2021/2/28 1:57 E問題を解説ACしました。
2021/3/2 0:15 燃やす埋めるの勉強をしたので、F問題を解説ACしました。
はじめに
キャディプログラミングコンテスト2021(AtCoder Beginner Contest 193) – AtCoder
A~Dの4完でした。
早解きがそこそこ成功して490位と黄パフォが出ました。
そして…
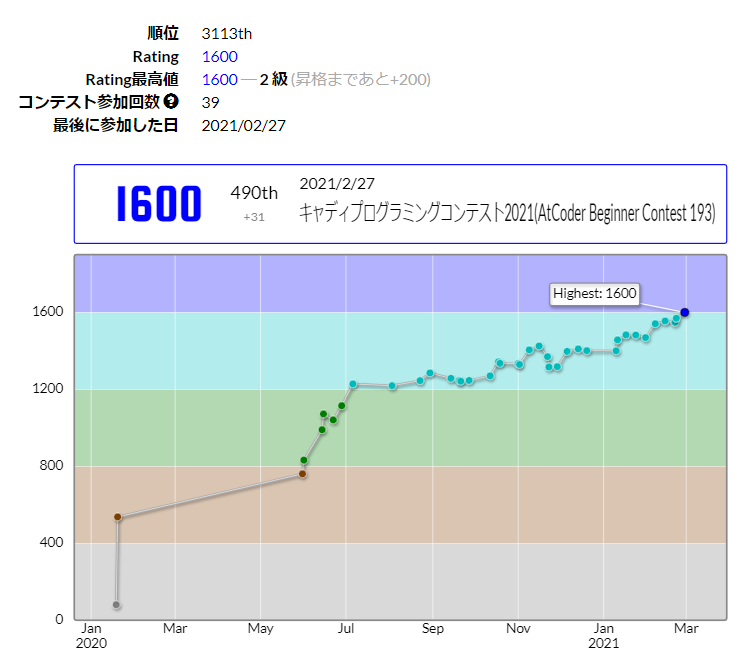
青色になれました!
色変記事もまた書こうと思います。一先ずの目標達成ですね。
明日からはレートを気にせず気楽にやっていきたいと思います><
A – Discount
Aにしてはややこしくないですか?
B/Aをすることで、その商品が何割になったかを知ることができます。
今回は何割引いたかを知りたいので、1-B/Aとして引いた分を計算します。
答えは百分率なので*100を考慮してACです。
#include<bits/stdc++.h>
using namespace std;
int main(){
double A,B;
cin>>A>>B;
printf("%.10f\n",100-(B/A)*100);
}
B – Play Snuke
問題文がややこしい….。
0.5,1.5,2.5…に1台ずつ減るので、A分かけてその店に行ったときはA台減っているはずです。
在庫はX台あるので、X-Aが0以下になった時は在庫がないといえます。
なので、X-A>0である店があるか探索し、ある場合はその中で最も小さいPが答えになります。
ない場合は買えないので-1が答えになります。
#include<bits/stdc++.h>
using namespace std;
int main(){
int N;
cin>>N;
int ans=INT_MAX;
for(int i=0;i<N;i++){
int A,P,X;
cin>>A>>P>>X;
int n=X-A;
if(n>0) ans=min(ans,P);
}
if(ans==INT_MAX) cout<<"-1"<<endl;
else cout<<ans<<endl;
}
C – Unexpressed
a=2、N=10^10であったとしても、b=34あたりでa^bはNを越えます。
こんな感じでa^bと表せれる数はかなり小さいので全探索で良さそうです。
aの範囲はbが最低でも2であることから、√Nまで探索すればOKです。
#include<bits/stdc++.h>
using namespace std;
int main(){
long long N;
cin>>N;
set<long long> s;
for(long long i=2;i<sqrt(N)+1;i++){
for(long long j=2;;j++){
long long n=pow(i,j);
if(n>N) break;
s.insert(n);
}
}
cout<<N-s.size()<<endl;
}
D – Poker
S,Tのそれぞれ5文字目が#(不確定文字)で、文字のパターンは1~9しかないため全探索で良さそうです。
問題は、#を決めたときにそうなるパターンが幾つあるかです。
K=2 S=1144# T=2233# の場合、Sの#=9,Tの#=8とする 9は残り札が2枚あるので2通り、8は残り札が2枚あるので2通り なのでこのパターンは2*2で4通りある。 Sの#=1,Tの#=8とすると 1は残り札0枚なので0通りとなり、このパターンは0通りになる
と、残り札から計算することができます。
注意はSの#=Tの#のときです。
片方が確定した時、もう片方は残り札がさらに1枚少なくなります。
#include<bits/stdc++.h>
using namespace std;
int main(){
long long K;
cin>>K;
string S,T;
cin>>S>>T;
int c[10]={0};
for(int i=0;i<4;i++){
c[S[i]-'0']++;
c[T[i]-'0']++;
}
long long cnt=0;
long long sum=0;
for(int i=1;i<=9;i++){
for(int j=1;j<=9;j++){
if(i==j&&c[i]+2>K) continue;
if(c[i]+1>K) continue;
if(c[j]+1>K) continue;
//cout<<i<<","<<j<<"---"<<c[i]<<","<<c[j]<<endl;
long long sc1=0,sc2=0;
for(int k=1;k<=9;k++){
long long cn=0;
if(i==k) cn++;
for(int l=0;l<4;l++){
if(S[l]-'0'==k) cn++;
}
sc1+=k*pow(10,cn);
}
for(int k=1;k<=9;k++){
long long cn=0;
if(j==k) cn++;
for(int l=0;l<4;l++){
if(T[l]-'0'==k) cn++;
}
sc2+=k*pow(10,cn);
}
long long nx;
if(i!=j) nx=(K-c[i])*(K-c[j]);
else nx=(K-c[i])*(K-c[i]-1);
//cout<<i<<","<<j<<","<<"---"<<sc1<<","<<sc2<<"---"<<sum<<","<<cnt<<","<<nx<<endl;
sum+=nx;
if(sc1>sc2){
cnt+=nx;
}
}
}
printf("%.10f\n",(double)cnt/sum);
}
高橋君が勝つ確率は、
高橋君の勝つパターン数/総パターン数
です。点数が高橋君>青木君である場合にのみ、高橋君の勝つパターン数を加算し
点数に限らず総パターン数を加算します。
E – Oversleeping
問題文を電車と、睡眠に分けて整理します。
電車:[X,X+Y),[3X+2Y,3X+3Y)...[(2n-1)X+(2n-2)Y,(2n-1)X+(2n-1)Y) の範囲を満たすとき、電車はB駅に停車している。 このとき、各区間が2X+2Y周期でループすると考え、 X <= t mod (2X+2Y) < X+Y を満たすtのとき、電車はB駅に停車するといえる。
睡眠:[P,P+Q),[2P+Q,2P+2Q)...[nP+(n-1)Q,nP+nQ) の範囲を満たすとき、起きている。 このとき、各区間がP+Qでループすると考え、 P <= t mod (P+Q) < P+Q を満たすtのとき、起きているといえる。
2つの条件が出てきました。この2つの条件tを満たす時間の最小が答えとなります。
中国余剰定理
複数のmod式が成り立つかどうかに関連する定理として中国余剰定理というものがあります。
細かい説明はWikipediaとかに任せるとして…ざっと説明すると、
x = r1 mod m1 x = r2 mod m2 ... x = rn mod mn を満たすxを求める
これを解くライブラリがACLにあるそうです。
vectorのrとmにそれぞれ求めたいmod式を詰め込みます。
返り値はpair型で、今回重要になるのはfirstの方になります。(firstがxの値)
firstが0の場合、解なしとなります。
範囲をイコールの式にしましょう
中国余剰定理は見ての通り、イコールの式で使う定理です。
今回のmod式は範囲となっています。困りました…。
ここで制約を見てみましょう。
1≤T≤10 1≤X≤10^9 1≤Y≤500 1≤P≤10^9 1≤Q≤500
YとQの値がかなり小さいです。
ACLの中国余剰定理を解くライブラリはO(nlog(lcm(m))で動きます。
nは今回2つの式なので2、lcm(m)は大きくなりそうですがlogがあるので高く見ても50程度でしょう。
Y*Qの2.5*10^5回を全通り回しても十分高速に動きます。
なので、条件の範囲を全て調べ、その中で最小である答えを選べばOKです。
X <= t mod (2X+2Y) < X+Y,P <= t mod (P+Q) < P+Q なら、 X = t mod (2X+2Y) X+1 = t mod (2X+2Y) ... X+Y-1 = t mod (2X+2Y) と P = t mod (P+Q) P+1 = t mod (P+Q) ... P+Q-1 = t mod (P+Q) の全組み合わせを試すことで、範囲の全パターンを網羅する。
#include<bits/stdc++.h>
//#include<boost/multiprecision/cpp_int.hpp>
#include<atcoder/all>
using namespace std;
//using namespace boost::multiprecision;
using namespace atcoder;
int main(){
int T;
cin>>T;
while(T-->0){
long long X,Y,P,Q;
cin>>X>>Y>>P>>Q;
//P寝てQ起きる
//P<=ans mod (P+Q) < P+Q
//移動にX秒Y秒停車
//X <= ans mod (2X+2Y) <X+Y
long long ans=LLONG_MAX;
for(long long i=0;i<Q;i++){
for(long long j=0;j<Y;j++){
vector<long long> r,m;
r.push_back(P+i);
m.push_back(P+Q);
r.push_back(X+j);
m.push_back(2*X+2*Y);
pair<long long,long long> p;
p=crt(r,m);
//cout<<p.first<<","<<p.second<<endl;
if(p.first!=0) ans=min(ans,p.first);
}
}
if(ans==LLONG_MAX) cout<<"infinity"<<endl;
else cout<<ans<<endl;
}
}
F – Zebraness
解説ありきですが、燃やす埋めるという手法で解けるらしいです。
燃やす埋めると仲良くなる1 | ぬるからの雑記帳 (nullkara.jp)
昨日少し勉強したら、とりあえず解説ACまで持っていけるようになりました。
グラフを作って考える-最大カット
2 WB B?
という入力を考えます。
各マスを頂点として、sから伸びる線は白に塗る、tに伸びる線は黒に塗るとします。
一先ず、しまう度のことは考えずに白黒に塗り分けることを考えます。
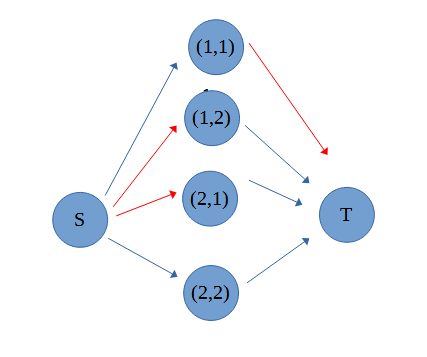
赤い線はコスト-∞、青い線はコスト0です。
黒いマスは白色で塗れないため、sから伸びる線をコスト-∞とし最大カットの際に選択させないようにします。
?のマスは両方に塗れるため、sからの線もtへの線もコスト0です。
これに、しまう度を入れていきます。
隣り合うマスが違う色であれば、しまう度は1増えるのでこうすれば良さそうです。
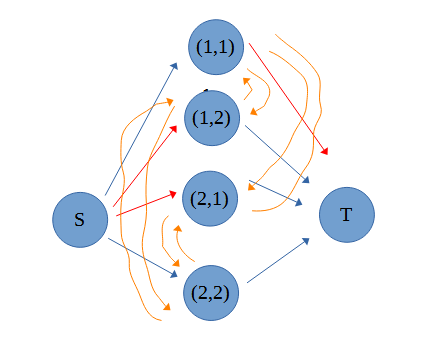
追加されたオレンジの線が、コスト1のしまう度増加用の線で、隣り合ったマスに伸ばすように引いています。
例えば、(1,1)が白で(1,2)が黒である場合、s->(1,2)->(1,1)->tというルートが残ってしまい、-∞を避けて切るにはコスト1の線を切るしか仕方がなくなります。
(1,1)が白で(1,2)も白である場合、(1,1)と(1,2)に入っていく線(s->の線)が切れているため、この2つを繋ぐオレンジの線を切らなくてもルートが遮断されます。
こんな感じで最大カットのグラフが出来上がりました。
グラフを作って考える-最小カット
最大カットはNP完全であるため、最小カットに言い換えましょう。
初期値を考えられる最大のしまう度とし、隣り合った色が同じ場合に1点引かれるとします。
赤線は+∞のコストがかかるとして、言い換えられそうです。
ただ、このままだと損失のオレンジの線が引けなくなってしまいます。
同じ色で減点なので、s->XX->XX->sというルートかt->XX->XX->tというルートを作ってやりたいのですが、sに入る線はなくtから出る線はないため不可能です。
最大カットのようにsからtへ流していきたいので、問題を次のように言い換えます。
市松で塗った時の片方の色を逆転させる 逆転させたので隣り合う色の関係も逆転し、違う色なら1点引かれるとなる
(x,y)のx+yが偶数のマスの色を逆転させると考えると、グラフは
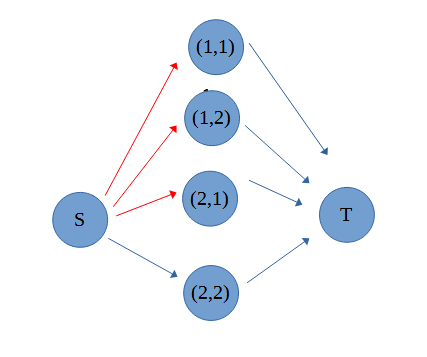
のようになりました。
(1,1)の色が反転したため、赤線と青線の位置が切り替わっています。
(2,2)は?マスでどっちの色にも濡れるため、反転しても変化なしです。
この操作により、”違う色なら1点引かれる”と最大カットと同じような条件になりました。なので、
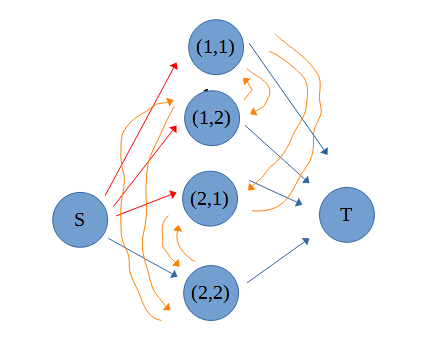
同じように隣り合うマスに線を引いてやることで損失を表現することができます。
これに対して最小カットを求め、初期点(最大のしまう度)から引くことで答えとなります。
ちなみに、上記グラフの場合(1,1),(1,2),(2,1)は->t側が切れているので、(2,2)も同じように->t側を切ることでコスト0でカットすることができます。
t側は黒色ですが、(2,2)は色反転しているので白色に塗ればOKです。最大のしまう度は4で、最小カットの答えが0なので、この例題の答えは4となります。
ソースコード
上記の考えをソースコードに落とします。
実装にはACLの最大流のライブラリを使いました。
#include<bits/stdc++.h>
//#include<boost/multiprecision/cpp_int.hpp>
#include<atcoder/all>
using namespace std;
//using namespace boost::multiprecision;
using namespace atcoder;
int main(){
long long N;
cin>>N;
mf_graph<long long> g(N*N+2);
long long s=N*N;
long long t=N*N+1;
string S[N];
for(int i=0;i<N;i++){
cin>>S[i];
}
long long sum=0;
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
//最大のしまう度計算
long long c=2;
if(i==0) c--;
if(j==0) c--;
sum+=c;
//隣り合うマスに1損失を引く
if(i!=0) g.add_edge(i*N+j,(i-1)*N+j,1);
if(i!=N-1) g.add_edge(i*N+j,(i+1)*N+j,1);
if(j!=0) g.add_edge(i*N+j,i*N+j-1,1);
if(j!=N-1) g.add_edge(i*N+j,i*N+j+1,1);
//sとtが別のグラフになるので
//市松で塗った時の片方だけ黒白の辺を反転する
if((i+j)%2==0){
//s->が黒で、->tが白
if(S[i][j]=='W') g.add_edge(s,i*N+j,10000000);
else g.add_edge(s,i*N+j,0);
if(S[i][j]=='B') g.add_edge(i*N+j,t,10000000);
else g.add_edge(i*N+j,t,0);
}
else{
//s->が白で、->tが黒
if(S[i][j]=='B') g.add_edge(s,i*N+j,10000000);
else g.add_edge(s,i*N+j,0);
if(S[i][j]=='W') g.add_edge(i*N+j,t,10000000);
else g.add_edge(i*N+j,t,0);
}
}
}
//cout<<sum<<endl;
cout<<sum-g.flow(s,t)<<endl;
}
long long c=2;
if(i==0) c--;
if(j==0) c--;
sum+=c;
が最大のしまう度の計算で、市松に塗られた時の値を計算しています。
//隣り合うマスに1損失を引く
if(i!=0) g.add_edge(i*N+j,(i-1)*N+j,1);
if(i!=N-1) g.add_edge(i*N+j,(i+1)*N+j,1);
if(j!=0) g.add_edge(i*N+j,i*N+j-1,1);
if(j!=N-1) g.add_edge(i*N+j,i*N+j+1,1);
は解説中のオレンジの線で、1の損失を表したものです。
隣り合うマスに対して引きます。
//sとtが別のグラフになるので
//市松で塗った時の片方だけ黒白の辺を反転する
if((i+j)%2==0){
//s->が黒で、->tが白
if(S[i][j]=='W') g.add_edge(s,i*N+j,10000000);
else g.add_edge(s,i*N+j,0);
if(S[i][j]=='B') g.add_edge(i*N+j,t,10000000);
else g.add_edge(i*N+j,t,0);
}
else{
//s->が白で、->tが黒
if(S[i][j]=='B') g.add_edge(s,i*N+j,10000000);
else g.add_edge(s,i*N+j,0);
if(S[i][j]=='W') g.add_edge(i*N+j,t,10000000);
else g.add_edge(i*N+j,t,0);
}
s->の線と->tの線を引く処理です。
市松の片方を反転させるため、(x,y)のx+yが偶数か奇数かで条件分岐しています。
また、黒である場所を白で塗る、白である場所を黒で塗るは不可能なため∞として大きな値を入れています。
?の場合は両方濡れるのでs->と->tの両方に0の辺を張っています。
解説しながら自分の考えに矛盾がなかったので、少なくともこの問題は理解できたのですが….
類題を解けと言われると無理ですね…。まず、燃やす埋めるの問題だと気付けないです。
おわりに
Atcoder青ということで一区切りついたので、他のコンテンツも力を入れたいです。
今のところやりたいのは、
●Project Euler
●AOJ ICPC
●Herbert
Welcome to Herbert Online Judge (tealang.info)
この辺りですかね…。
あと、Atcoder ProblemsのBoot camp for Beginnersも埋めたいですね。
(今のところ、Easy/Medium/Hardが54/23/24)
Kaggleもやりたいし、ヒューリスティックコンテストも頑張りたいのです><
(と、色々やりたいことだけ増えてます><)


コメント