燃やす埋めると仲良くなる1

先日開催されたABC193のF問題

F – Zebraness (atcoder.jp)

燃やす埋めると呼ばれる問題なのですが、解説を見ても分からず…。
少し勉強して仲良くなることにしました。

E – MULを解いてみる
まとめ

E – MULを解いてみる

E – MUL (atcoder.jp)

燃やす埋めるで解ける典型的な問題らしいのでこれを解いてみます。

グラフで考える-最大カット

入力例1を以下のようなグラフで考えます。
※xの倍数を割るという制約は考えずに、一旦好きに割れるとして考える。

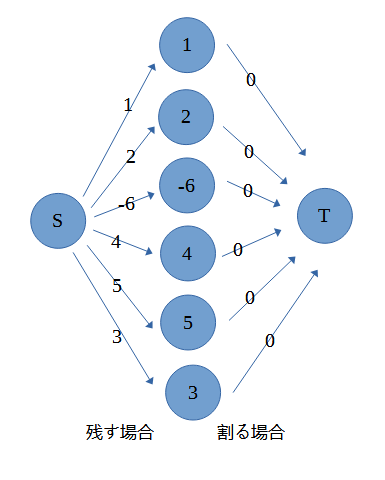
真ん中は各宝石を表していて、Sから伸びる線を切ること=その宝石を残す、Tに伸びる線を切ること=その宝石を潰す
としたとき、このグラフに対して最大カットを求めることで答えが導けます。
この場合、-6は割る線を切って、他は残す線を切るのが最適ですね。

グラフで考える-最小カット

ただし、最大カットはNP完全で高速に解けません。
どうしましょう？

実は最小カットと呼ばれる、最小を求めるほうは高速なアルゴリズムがあります。
なのでこの問題を、いかに罰金を少なくするかと言い換えることで最小カットに帰着させます。
具体的には、割ることで本来得られる宝石の価値がなくなると言い換えます。

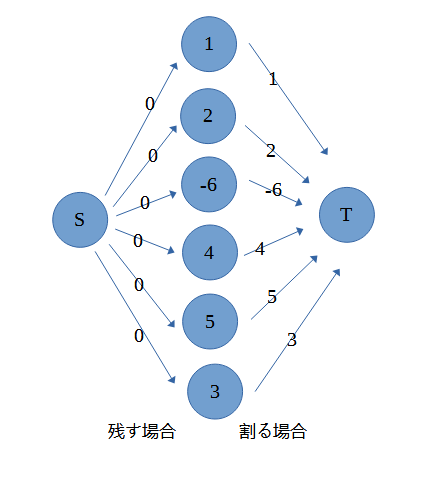
最小カットを解くアルゴリズムは負の重みの辺がある場合は使えません。困りました。
-6のところですが、この宝石は残せば6罰金になります。
なので、残す場合の方の辺に重さ6として移すことができます。(残すor割るの罰金額を辺の重さにしているので)

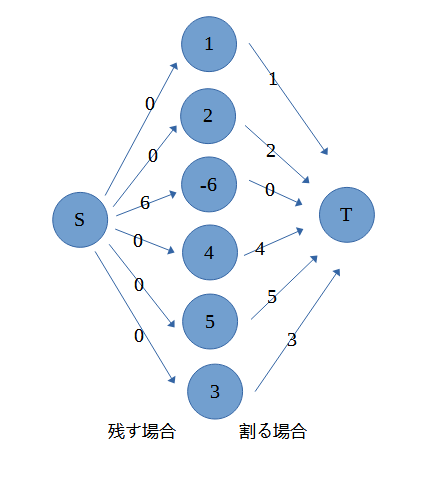
という訳でこんなグラフになります。
今の状態では0の辺を選んで切る=罰金0が最小カットになります。

xの倍数だけ割れるを考慮

2番目の割るを選択した場合、4,6,8,10…番目の割るを選択するようにグラフを変える必要があります。
答えありきですが、以下のようにします。

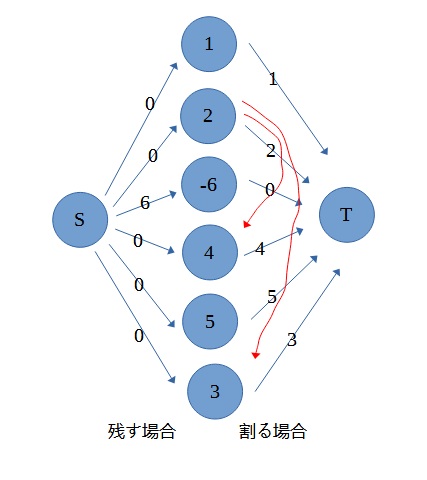
2,4,6番目の宝石に赤い線が追加されました。
赤い線は罰金∞の線です。つまり最小カットとして含むとNGとなる線になります。
こうすることで何が嬉しいかというと、2番目の宝石を割った際にS→2番目→4番目→Tと経路ができます。
このとき、S→2番目は2番目を割るとしているため選択不可、2番目→4番目は∞罰金なので選択不可となり、4番目→Tを選択するしかない(4番目を割るしかない)となります。
逆に2番目を残すとした場合、2番目から出ている赤い線を辿る経路がなくなるので4番目の線は自由に切ることができます。
これを、他の宝石にも適用し、

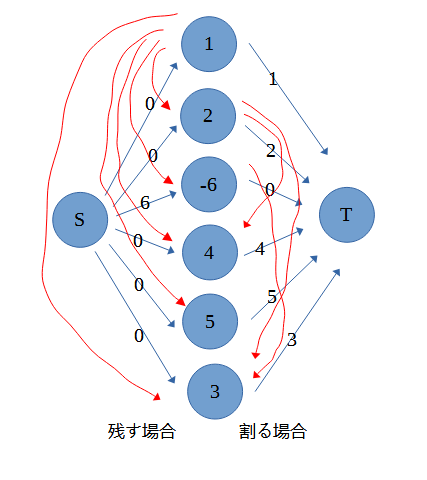
このグラフの最小カットを求めることで罰金の最小を求めることができます。
得られる最大のお金は正の宝石の総和である、15であるため15-最小カットの答えがこの入力自体の答えになります。

コーディング

https://atcoder.github.io/ac-library/master/document_ja/maxflow.html

最小カットは最大フローを解くことで得られます。
ACLには最大フローを解くライブラリがあるので使いましょう。

    long long N;
    cin>>N;

    mf_graph<long long> g(N+2);
    long long s=N;
    long long t=N+1;

グラフのサイズは2つ分余計に取ります。
宝石の頂点N個＋スタートとゴールの頂点が2つ必要だからです。

    long long sum=0;
    for(int i=0;i<N;i++){
        long long a;
        cin>>a;
        if(a<0){
            g.add_edge(s,i,-a);
            g.add_edge(i,t,0);
        }
        if(a>0){
            sum+=a;
            g.add_edge(s,i,0);
            g.add_edge(i,t,a);
        }
    }

負の場合は残すと罰金なのでsからの線に値を追加、正の場合は潰すと罰金なのでtへの線に追加します。
罰金がない場合の金額もこのときに計算します。

    for(int i=1;i<=N;i++){
        for(int j=i+i;j<=N;j+=i){
            g.add_edge(i-1,j-1,1000000000000);
        }
    }

xの倍数しか潰せなくするための∞辺を追加します。
プログラム的にはとても大きい数、具体的には各辺であり得る値より大きい値にします。(今回の場合は10^9+1より大きくする)
注意はLLONG_MAXとかにしないことです。最大流の計算途中でオーバーフローが発生し、正しく計算できない可能性があります。ほどほどに大きい数にしましょう。

cout<<sum-g.flow(s,t)<<endl;

フローを流して罰金の最小金額を求めて終わりです。
纏めると以下のようなコードになりました。

#include<bits/stdc++.h>
//#include<boost/multiprecision/cpp_int.hpp>
#include<atcoder/all>

using namespace std;
//using namespace boost::multiprecision;
using namespace atcoder;

int main(){
    long long N;
    cin>>N;

    mf_graph<long long> g(N+2);
    long long s=N;
    long long t=N+1;

    long long sum=0;
    for(int i=0;i<N;i++){
        long long a;
        cin>>a;
        if(a<0){
            g.add_edge(s,i,-a);
            g.add_edge(i,t,0);
        }
        if(a>0){
            sum+=a;
            g.add_edge(s,i,0);
            g.add_edge(i,t,a);
        }
    }

    for(int i=1;i<=N;i++){
        for(int j=i+i;j<=N;j+=i){
            g.add_edge(i-1,j-1,1000000001);
        }
    }

    cout<<sum-g.flow(s,t)<<endl;
}

コード自体は簡単に見えますが、考え方的にはすごくややこしいです。