競プロ参加記028 AtCoder Beginner Contest 185 (ABC185)

Atcoder

2020/12/14 1:17 解説放送を見て、E問題解きなおし

はじめに

AtCoder Beginner Contest 185 – AtCoder

A,B,C,D,E,Fの6完でした($・・)/~~~
初の全完ですよ！良かったです。
(前回のABCが2完で死んでたので、何とか取り戻した感じです。)

A – ABC Preparation

A – ABC Preparation (atcoder.jp)

同じ問題案は 1度しか使えないかつ、それぞれの問題が1つ必要。
なので、A1～A4の最小値が答えになります。

#include<bits/stdc++.h>
//#include<atcoder/all>

using namespace std;
//using namespace atcoder;

int main(){
    int A[4];
    cin>>A[0]>>A[1]>>A[2]>>A[3];
    sort(A,A+4);
    cout<<A[0]<<endl;
}

C++のsortは昇順にソートされるため、0番目の値を出力すると最小になります。

B – Smartphone Addiction

B – Smartphone Addiction (atcoder.jp)

問題文が微妙にややこしいですが、入力例が親切です。
私はこの手の問題は問題文をあまり読まず、入力例から読み込んでいくようにしています。(今回もそうしました)

#include<bits/stdc++.h>
//#include<atcoder/all>

using namespace std;
//using namespace atcoder;

int main(){
    int N,M,T;
    cin>>N>>M>>T;

    int fN=N;
    int A,B;
    int t=0;
    for(int i=0;i<M;i++){
        cin>>A>>B;
        N-=A-t;
        if(N<=0){
            cout<<"No"<<endl;
            return 0;
        }
        N+=B-A;
        N=min(N,fN);
        t=B;
    }
    N-=T-t;
    if(N<=0){
        cout<<"No"<<endl;
        return 0;
    }
    cout<<"Yes"<<endl;
}

Bにしては少しややこしい気がしますが、あらゆるコーナーケースが入力例にあるのが優しいところですね。

C – Duodecim Ferra 

C – Duodecim Ferra (atcoder.jp)

長さLの場合、切断できる箇所はL-1個あります。
今回3を(2,1)で分けるのと、(1,2)で分けるのでは違うとしているため、このL-1個の切断箇所から11箇所選ぶ通りが答えになります。
順番は関係ないのでコンビネーションを使います。
注意点は、64bit整数でもコンビネーションの計算でオーバーフローする場合があります。(全部掛けてから割るなどの場合)
私は多倍長で殴りました。

#include<bits/stdc++.h>
#include<boost/multiprecision/cpp_int.hpp>
#include<atcoder/all>

using namespace std;
using namespace boost::multiprecision;
//using namespace atcoder;

int main(){
    cpp_int  N;
    cin>>N;
    N--;
  
    cpp_int ans=1;
    for(int i=1;i<=11;i++){
        //cout<<(N-i+1)<<endl;
        ans*=(N-i+1);
    }

    for(int i=1;i<=11;i++){
        ans/=i;
    }

    cout<<ans<<endl;
}

D – Stamp

D – Stamp (atcoder.jp)

kを大きくすれば大きくするほど押す回数が少なくなります。
ただ、大きすぎると青マスを押してしまう可能性があります。
なので最適なkは、青を押さない範囲で最大の数。となります。
青を押さない範囲=kは全ての白の連続区間の長さ以下
と言い換えられます。(kは最小の連続区間の長さ以下)

ある白の連続区間の長さをWとした場合、できるだけ被らずにハンコを押すのが最適のため、赤に塗る回数はW/k…と言いたいですが、W=5,k=2などの場合に端数を塗るための1回がでてきます。
そのため、ハンコを押す回数はW/k+(端数があるなら1)となります。
これを、全ての白の連続区間で計算します。

#include<bits/stdc++.h>
//#include<atcoder/all>

using namespace std;
//using namespace atcoder;

int main(){
    int N,M;
    cin>>N>>M;

    int A[M+1];
    for(int i=0;i<M;i++){
        cin>>A[i];
    }
    A[M]=N+1;
    sort(A,A+M+1);

    int k=INT_MAX;
    int t=1;
    for(int i=0;i<M+1;i++){
        //cout<<A[i]<<","<<t<<endl;
        if(A[i]-t!=0){
            k=min(k,A[i]-t);
        }
        t=A[i]+1;
    }
    int ans=0;
    t=1;
    for(int i=0;i<M+1;i++){
        ans+=(A[i]-t)/k+((A[i]-t)%k!=0);
        t=A[i]+1;
    }
    cout<<ans<<endl;
}

白の連続区間を数える際、カウントを1個進めて…みたいなことをするとTLEします。
青の位置Aiをソートし、そこから計算でO(1)で求めるようにしましょう。(0,N+1にも青ハンコがあるとして、AM+2で考えると端を考えなくて良くなり楽になります。)

E – Sequence Matching

E – Sequence Matching (atcoder.jp)

難問でした。
AtcoderProblem的にもE>Fでしたね。
Ai,Biを0番目(A0,B0)から見ていく場合、今見ているAのindexをa、Bのindexをbとして以下の3通りが考えられそうです。

Aaと同じBiの中で、b以上の中で1番indexが小さいものを合わせるように消す
Bbと同じAiの中で、a以上の中で1番indexが小さいものを合わせるように消す
AaもBbも不一致のまま次に進める

TLEコード

これをDFS(a,b,n)として遷移させていきました。
※nは現状のx+yの答え

Aaと同じBiの中で、b以上の中で1番indexが小さいものをbmとして　→　DFS(a+1,bm+1,n+bm-b) ※aとbmを合わせるため、bからbm-1の範囲を消した
Bbと同じAiの中で、a以上の中で1番indexが小さいものをamとして　→　DFS(am+1,b+1,n+am-a) ※bとamを合わせるため、aからam-1の範囲を消した
AaもBbも不一致のまま次に進める　→　DFS(a+1,b+1,n+1) ※aもbも進めて、不一致分の1を足す

下記コードになりました。

#include<bits/stdc++.h>
//#include<atcoder/all>

using namespace std;
//using namespace atcoder;

int N,M;
int A[1001];
int B[1001];
int ans=INT_MAX;
int ab[1001][1001];
void dfs(int a,int b,int n){
    //cout<<a<<","<<b<<","<<n<<","<<ab[a][b]<<endl;
    if(ab[a][b]!=-1){
        if(ab[a][b]<=n) return;
    }
    ab[a][b]=n;
    if(a>=N){
        ans=min(n+M-b,ans);
        return;
    }
    if(b>=M){
        ans=min(n+N-a,ans);
        return;
    }
    for(int i=b;i<M;i++){
        if(B[i]==A[a]){
            dfs(a+1,i+1,n+i-b);
        }
    }
    for(int i=a;i<N;i++){
        if(A[i]==B[b]){
            dfs(i+1,b+1,n+i-a);
        }
    }
    dfs(a+1,b+1,n+1);
}
int main(){
    cin>>N>>M;
    for(int i=0;i<N;i++){
        cin>>A[i];
    }
    for(int i=0;i<M;i++){
        cin>>B[i];
    }
    for(int i=0;i<=N;i++){
        for(int j=0;j<=M;j++){
            ab[i][j]=-1;
        }
    }
    dfs(0,0,0);
    cout<<ans<<endl;

}

一応メモ化もしたため、間に合うと思ったのですが…。
計算量が読め切らずTLEを出してしましました。

ACコードのために_二分探索編

    for(int i=b;i<M;i++){
        if(B[i]==A[a]){
            dfs(a+1,i+1,n+i-b);
        }
    }

ここの探索がちょっと無駄です。
あらかじめ各数字のindexをvectorに持っておき、それをsortしておけばupper_noundで探索できます。
具体的に、

map<int,vector<int>> Am,Bm;

Ai,Biの最大が10^9なのでmapで持って、

    for(int i=0;i<N;i++){
        cin>>A[i];
        Am[A[i]].emplace_back(i);
        sort(Am[A[i]].begin(),Am[A[i]].end());
    }

入力の際に、格納とソートを行い、

    if(Bm.find(A[a])!=Bm.end()){
        auto Bma=Bm[A[a]];
        auto it=upper_bound(Bma.begin(),Bma.end(),b-1);
        if(it!=Bma.end()){
            int i=*it;
            //cout<<*it<<"-"<<i<<endl;
            dfs(a+1,i+1,n+i-b);
        }
 
    }

と、upper_bound(二分探索)で高速化するようにしました。
TLE数は減りましたが、まだダメでした。

ACコードのために_priority_queue

過去の経験から、この手のメモ化を使った探索はpriority_queueを使って最善になりそうな手順(今回は、nが小さい順)からやると早くなります。(悪い手のまま奥に潜りにくくなる)
DFS(a,b,n)を、priority_queue<pair<n,pair<a,b>>>として遷移させるようにしました。
注意点は、priority_queueは降順ソートされるっぽいことです。graterで昇順ソートさせる方法もあるのですが、この時終了5分前くらいで焦っていたので、負を掛けて反転させることとしました。

#include<bits/stdc++.h>
//#include<atcoder/all>

using namespace std;
//using namespace atcoder;
#pragma GCC target("avx2")
#pragma GCC optimize("O3")
#pragma GCC optimize("unroll-loops")

int N,M;
int A[1001];
int B[1001];
map<int,vector<int>> Am,Bm;
int ans=INT_MAX;
int ab[1001][1001];

int main(){
    ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    cin>>N>>M;
    for(int i=0;i<N;i++){
        cin>>A[i];
        Am[A[i]].emplace_back(i);
        sort(Am[A[i]].begin(),Am[A[i]].end());
    }
    for(int i=0;i<M;i++){
        cin>>B[i];
        Bm[B[i]].emplace_back(i);
        sort(Bm[B[i]].begin(),Bm[B[i]].end());
    }
    for(int i=0;i<=N;i++){
        for(int j=0;j<=M;j++){
            ab[i][j]=-1;
        }
    }
    priority_queue<pair<int,pair<int,int>>> q;
    q.push(make_pair(0,make_pair(0,0)));
    while(!q.empty()){
        int a=q.top().second.first;
        int b=q.top().second.second;
        int n=q.top().first;
        n=-n;
        q.pop();
        //cout<<a<<","<<b<<","<<n<<","<<ab[a][b]<<endl;
        if(ab[a][b]!=-1){
            if(ab[a][b]<=n) continue;
        }
        ab[a][b]=n;
        if(a>=N){
            ans=min(n+M-b,ans);
            continue;
        }
        if(b>=M){
            ans=min(n+N-a,ans);
            continue;
        }
        if(Bm.find(A[a])!=Bm.end()){
            auto Bma=Bm[A[a]];
            auto it=upper_bound(Bma.begin(),Bma.end(),b-1);
            if(it!=Bma.end()){
                int i=*it;
                //cout<<*it<<"-"<<i<<endl;
                q.push(make_pair(-(n+i-b),make_pair(a+1,i+1)));
            }

        }
        if(Am.find(B[b])!=Am.end()){
            auto Ama=Am[B[b]];
            auto it=upper_bound(Ama.begin(),Ama.end(),a-1);
            if(it!=Ama.end()){
                int i=*it;
                //cout<<*it<<"-"<<i<<endl;
                q.push(make_pair(-(n+i-a),make_pair(i+1,b+1)));
            }

        }
        q.push(make_pair(-(n+1),make_pair(a+1,b+1)));
    }
    cout<<ans<<endl;

}

これで何とかACです。
定数倍高速化で乗り切ろうとした形跡がコードにありますが、無駄にWAが増えるだけなのでこの癖直したいところです…。

解説放送を見て少し整理

解説放送を見てましたが、遷移を以下のようにしていました。

A[a]==B[b]なら、一致したとして進める。
そうでないなら、
　・A[a]を削除してaを1進める
　・B[b]を削除してbを1進める
　・A[a]とB[b]を不一致として進める

これだと、単純なBFSでもコストが1増えながらバラけるため良さそうですね。

#include<bits/stdc++.h>
//#include<atcoder/all>

using namespace std;
//using namespace atcoder;

int N,M;
int A[1001];
int B[1001];
int ans=INT_MAX;
int ab[1001][1001];

int main(){
    cin>>N>>M;
    for(int i=0;i<N;i++){
        cin>>A[i];
    }
    for(int i=0;i<M;i++){
        cin>>B[i];
    }
    for(int i=0;i<=N;i++){
        for(int j=0;j<=M;j++){
            ab[i][j]=-1;
        }
    }

    queue<pair<int,pair<int,int>>> q;
    q.push(make_pair(0,make_pair(0,0)));
    while(!q.empty()){
        int a=q.front().second.first;
        int b=q.front().second.second;
        int n=q.front().first;
        q.pop();
        if(ab[a][b]!=-1){
            if(ab[a][b]<=n) continue;
        }
        ab[a][b]=n;
        if(a>=N){
            ans=min(n+M-b,ans);
            continue;
        }
        if(b>=M){
            ans=min(n+N-a,ans);
            continue;
        }
        if(A[a]!=B[b]){
            q.push(make_pair(n+1,make_pair(a+1,b)));
            q.push(make_pair(n+1,make_pair(a,b+1)));
            q.push(make_pair(n+1,make_pair(a+1,b+1)));
        }
        else q.push(make_pair(n,make_pair(a+1,b+1)));
    }
    cout<<ans<<endl;

}

かなり綺麗なメモ化BFSになったかと思います。

F – Range Xor Query

F – Range Xor Query (atcoder.jp)

知ってれば解ける問題です。所謂ライブラリ問題、典型問題というやつです。
xorのように計算順序はどうでもいい計算(A xor B xor CもA xor C xor Bも答えは同じ)を区間に対して行う問題は、大体セグ木で解決します。

#include<bits/stdc++.h>
//#include<atcoder/all>

using namespace std;
//using namespace atcoder;

//https://algo-logic.info/segment-tree/#toc_id_3_2
template <typename X>
struct SegTree {
    using FX = function<X(X, X)>; // X•X -> X となる関数の型
    int n;
    FX fx;
    const X ex;
    vector<X> dat;
    SegTree(int n_, FX fx_, X ex_) : n(), fx(fx_), ex(ex_), dat(n_ * 4, ex_) {
        int x = 1;
        while (n_ > x) {
            x *= 2;
        }
        n = x;
    }
    void set(int i, X x) { dat[i + n - 1] = x; }
    void build() {
        for (int k = n - 2; k >= 0; k--) dat[k] = fx(dat[2 * k + 1], dat[2 * k + 2]);
    }
    void update(int i, X x) {
        i += n - 1;
        dat[i] = x;
        while (i > 0) {
            i = (i - 1) / 2;  // parent
            dat[i] = fx(dat[i * 2 + 1], dat[i * 2 + 2]);
        }
    }
    X query(int a, int b) { return query_sub(a, b, 0, 0, n); }
    X query_sub(int a, int b, int k, int l, int r) {
        if (r <= a || b <= l) {
            return ex;
        } else if (a <= l && r <= b) {
            return dat[k];
        } else {
            X vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
            X vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
            return fx(vl, vr);
        }
    }
};

int main(){
    int N,Q;
    cin>>N>>Q;
    auto fx = [](int x1, int x2) -> int { return x1^x2; };
    int ex = 0;
    SegTree<int> rmq(N+5, fx, ex);

    for(int i=1;i<=N;i++){
        int A;
        cin>>A;
        rmq.update(i,A);
    }

    for(int i=0;i<Q;i++){
        int T,X,Y;
        cin>>T>>X>>Y;
        if(T==1){
            rmq.update(X,rmq.query(X,X+1)^Y);
        }
        else{
            cout<<rmq.query(X,Y+1)<<endl;
        }
    }
}
セグメント木を徹底解説！0から遅延評価やモノイドまで | アルゴリズムロジック
セグメント木とは セグメント木とは、完全二分木（全ての葉の深さが等しい木）によって実装された、区間を扱うのに適したデータ構造のことです。 区間に対する操作を対数時間 O(log ...
algo-logic.info

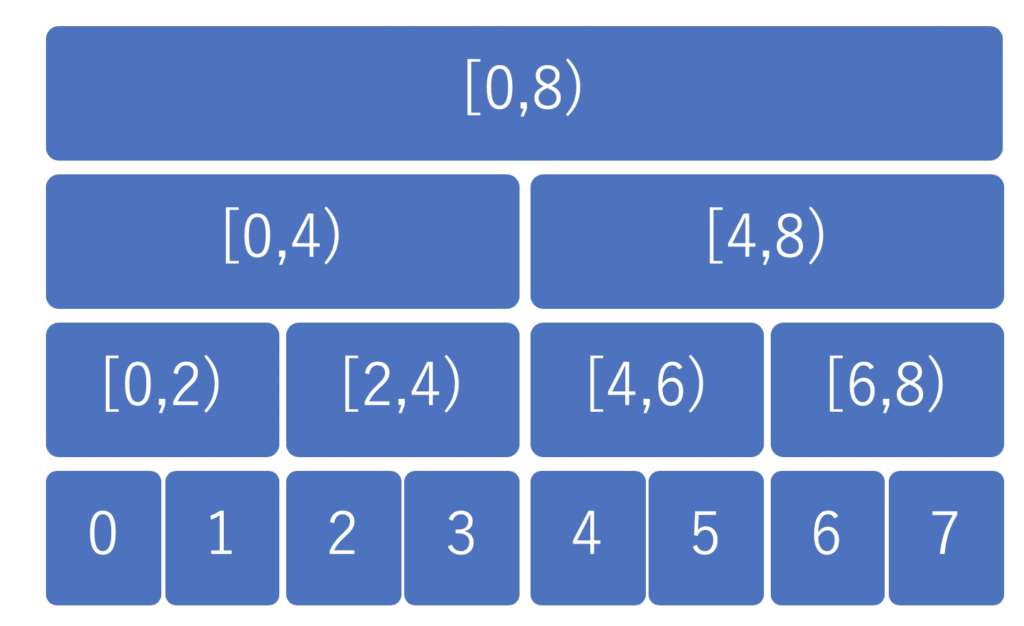
セグ木はこちらの”抽象化したセグメント木を実装する”から、お借りしました。
1点更新なので、遅延ではなく普通のセグ木でいいところも優しいところですね。

おわりに

全完したのに水パフォとは？(1521)
セグ木使えて、ややこしい動的計画法が解けて、数Bの素養がある…そんな人間が青になれないのは中々厳しいですね”(-“”-)”

コメント

タイトルとURLをコピーしました