2021/3/14 20:03に公開しましたが、まだ書きかけです。ごめんなさい><
AtCoder Heuristic Contest 001 – AtCoder
とうとう始まりました、ヒューリスティックコンテスト。
私も参加し、うんうん考えながら実装したので記録として残しておきます。
- 結果
- solver()
- solveMinKara()
- minHaiti()
- yakinamashi()
- largeRect(int mode=0)
- shortRect()
- donyoku()
- solveDonKara()
- colSqDo(int sx1,int sy1,int sx2,int sy2,int dx,int dy)
- colSqSq(int sx11,int sy11,int sx12,int sy12,int sx21,int sy21,int sx22,int sy22)
- OutRange(int i,int dx1=0,int dy1=0,int dx2=0,int dy2=0)
- hitSearch(int i,int dx1=0,int dy1=0,int dx2=0,int dy2=0)
- calcTotalP()
- calcSubmitScore()
- calcTotalScore()
- calcScore(int x1,int y1,int x2,int y2,int rs)
- inputCin()
- outputCout()
- inputFile(int no)
- timeCalc()
- checkTimer(double time)
- randxor()
- randxorsyosu()
- calcFace(int x1,int y1,int x2,int y2)
- main()
- ①点数をとりあえず獲得
- ②貪欲する
- ③テスト用の関数の作成
- ④山登り法
- ④焼きなまし法
- 最終提出
- やり残しと感想
結果
<TODO>点で<TODO>位でした。
最終的な提出コードは以下になります。
/*-----------------------------------------------------------------------------*/
//***コード作成者:NullKara (@NullKara)
//***AHC001提出用コード
//***スコア履歴
//2021-03-06 34353669666 (貪欲実装)
//2021-03-07 41669193424 (貪欲のバグ取り)
//2021-03-08 XXXXXXXXXXX (ペルソナ5Sやってました><)
//2021-03-09 47351351848 (山登り実装)
//2021-03-10 47760113117 (焼きなまし実装)
//2021-03-11 48691607253 (焼きなましパラメータ調整)
//2021-03-12 48809421892 (焼きなましパラメータ調整2)
//2021-03-13 XXXXXXXXXXX (Siralim Ultimateやってました><)
/*-----------------------------------------------------------------------------*/
/*Template-------------------------------------------------------------------------*/
#include<bits/stdc++.h>
using namespace std;
//https://atcoder.jp/contests/ahc001/submit
//https://kenkoooo.github.io/ahc001-gen-vis-wasm/
//https://shindannin.hatenadiary.com/entry/2021/03/06/115415
/*定数-----------------------------------------------------------------------------*/
const int ADSIZE=10000; //広告サイズ(固定)
const int NMAX=200; //広告の最大数
const long long MAXSCORE=1000000000; //最高点数
/*変数-----------------------------------------------------------------------------*/
//****AdData
int x[NMAX],y[NMAX],r[NMAX]; //x座標 y座標 大きさr x,yは+0.5なことに注意
int n; //広告の数
//****answer
int a[NMAX],b[NMAX],c[NMAX],d[NMAX]; //(a,b)~(c,d)の矩形
int amx[NMAX],bmx[NMAX],cmx[NMAX],dmx[NMAX]; //乱択時に使用。スコア最大時の座標を保持
int mxchg=-1; //!=-1ならmaxによる代入を最後行う
//****other
double TIME_LIMIT=4.85; //時間制限
int DCOUNTER=0; //デバッグ用カウンター
/*関数-----------------------------------------------------------------------------*/
//****宣言
//広告の位置を決める関数
void solver();
void solveMinKara();
void minHaiti();
void yakinamashi();
void largeRect(int mode=0);
void shortRect();
void donyoku();
void solveDonKara();
//当たり判定や、場外判定など
bool colSqDo(int sx1,int sy1,int sx2,int sy2,int dx,int dy);
bool colSqSq(int sx11,int sy11,int sx12,int sy12,int sx21,int sy21,int sx22,int sy22);
bool OutRange(int i,int dx1=0,int dy1=0,int dx2=0,int dy2=0);
bool hitSearch(int i,int dx1=0,int dy1=0,int dx2=0,int dy2=0);
//スコア計算
double calcTotalP();
void calcSubmitScore();
long long calcTotalScore();
double calcScore(int x1,int y1,int x2,int y2,int rs);
//I/O
void inputCin();
void outputCout();
void inputFile(int no);
//時間測定
double timeCalc();
void checkTimer(double time);
//その他計算
unsigned int randxor();
double randxorsyosu();
int calcFace(int x1,int y1,int x2,int y2);
//****実装
//メイン関数
int main(){
//mode切り替え
//提出時は1にする
int mode=2;
//mode0
//ファイルから50入力を読み込んでスコアを計算
//暫定スコアのものと同様
if(mode==0){
calcSubmitScore();
}
//mode1
//提出用。標準入力から読み込んだデータを標準出力で吐き出す。
else if(mode==1){
inputCin();
//開始時間の記録
timeCalc();
solver();
outputCout();
}
//mode2
//ファイルから1データ読み込んで標準出力で吐き出す。
else if(mode==2){
inputFile(16);
solver();
outputCout();
}
}
//この関数を読み込んで、答えを計算する
void solver(){
//modeを切り替えて、どのsolverを使うか切り替える。
int mode=2;
//mode1
//最少配置からの焼きなましを行う
if(mode==1){
solveMinKara();
}
//mode2
//貪欲配置からの焼きなましを行う
else if(mode==2){
solveDonKara();
}
}
//最少配置を行った後に焼きなましする
void solveMinKara(){
minHaiti();
yakinamashi();
}
//貪欲を行った後に焼きなましをする
void solveDonKara(){
donyoku();
shortRect();
largeRect(0);
largeRect(1);
largeRect(2);
largeRect(3);
yakinamashi();
}
//左上に伸ばす貪欲を行う
void donyoku(){
//左上の点から
vector<pair<int,int>> v;
for(int i=0;i<n;i++){
v.push_back(make_pair(x[i]+y[i],i));
}
//未配置のメモを付ける
for(int i=0;i<n;i++){
a[i]=-1;
}
//ソートする
sort(v.begin(),v.end());
for(int j=0;j<(int)v.size();j++){
int vidx=v[j].second;
int vx=x[vidx];
int vy=y[vidx];
int zx=vx,zy=vy;
//左上に伸ばしていく
//x,yどっちも
for(int k=2;;k++){
bool f=false;
for(int l=0;l<n;l++){
if(vx==x[l]&&vy==y[l]) continue;
if(colSqDo(vx-k,vy-k,vx,vy,x[l],y[l])) f=true;
if(a[l]!=-1&&colSqSq(vx-k,vy-k,vx,vy,a[l],b[l],c[l],d[l])) f=true;
}
if(vx-k<0||vy-k<0||f){
zx=vx-k+1;
zy=vy-k+1;
break;
}
}
//xだけ
for(int k=1;;k++){
bool f=false;
for(int l=0;l<n;l++){
if(vx==x[l]&&vy==y[l]) continue;
if(colSqDo(zx-k,zy,vx,vy,x[l],y[l])) f=true;
if(a[l]!=-1&&colSqSq(zx-k,zy,vx,vy,a[l],b[l],c[l],d[l])) f=true;
}
if(zx-k<0||zy<0||f){
zx=zx-k+1;
break;
}
}
//yだけ
for(int k=1;;k++){
bool f=false;
for(int l=0;l<n;l++){
if(vx==x[l]&&vy==y[l]) continue;
if(colSqDo(zx,zy-k,vx,vy,x[l],y[l])) f=true;
if(a[l]!=-1&&colSqSq(zx,zy-k,vx,vy,a[l],b[l],c[l],d[l])) f=true;
}
if(zx<0||zy-k<0||f){
zy=zy-k+1;
break;
}
}
//cout<<zx<<","<<zy<<","<<vx<<","<<vy<<endl;
//適用する
a[vidx]=zx;
b[vidx]=zy;
c[vidx]=vx+1;
d[vidx]=vy+1;
}
}
//最小配置を行う
void minHaiti(){
//ドットの周り1マスを囲うような広告配置
for(int i=0;i<n;i++){
a[i]=x[i];
b[i]=y[i];
c[i]=x[i]+1;
d[i]=y[i]+1;
}
}
//焼きなます
void yakinamashi(){
//現時点のスコアを保持
double mxsco=calcTotalP();
for(int i=0;i<n;i++){
amx[i]=a[i];
bmx[i]=b[i];
cmx[i]=c[i];
dmx[i]=d[i];
}
double nowsco=mxsco;
//最大保持のフラグを立てる
mxchg=1;
//初期温度と最終温度(st_temp->en_tempへ温度変化する)
//st_tempは最大点数、en_tempは最小点数がいいらしい
//微調整してこれくらいの値にした
double st_temp=0.05;
double en_temp=0;
//汎用カウンター
int count=0;
//checktimerで打ち切るまで焼きなましを行う
while(1){
//時間測定
double tm=timeCalc();
//時間がきたら打ち切る
checkTimer(tm);
//乱択変化の幅(時間経過で小さくしていく)
int haba=130.0 * (1.5 - (tm / TIME_LIMIT));
//乱択の結果を保持する変数を定義
int i,dx1,dy1,dx2,dy2;
//カウントアップ
count++;
DCOUNTER++;
//乱択適用後に、ルールに違反してないような入力が出るまでループする
while(1){
//乱数取得。ある広告の上下左右を伸び縮みさせる
i=count%n;//randxor()%n;
dx1=0;
dy1=0;
dx2=0;
dy2=0;
//平行移動
if(randxorsyosu()>0.90){
int tox=randxor()%haba-haba/2;
int toy=randxor()%haba-haba/2;
dx1=tox;
dy1=toy;
dx2=-tox;
dy2=-toy;
}
//伸び縮み
else{
double syo=randxorsyosu();
//1/3で縦だけ、横だけ、両方
if(syo<1.0/3.0){
dx1=randxor()%haba-haba/2;
dx2=randxor()%haba-haba/2;
}
else if(syo<2.0/3.0){
dy1=randxor()%haba-haba/2;
dy2=randxor()%haba-haba/2;
}
else {
dx1=randxor()%haba-haba/2;
dx2=randxor()%haba-haba/2;
dy1=randxor()%haba-haba/2;
dy2=randxor()%haba-haba/2;
}
}
//違反してないか確認
//自広告のドットが含まれるか
if(colSqDo(a[i]+dx1,b[i]+dy1,c[i]+dx2,d[i]+dy2,x[i],y[i])){
//範囲外か
if(!OutRange(i,dx1,dy1,dx2,dy2)){
//面積が指定より超えるような入力は許容しない
if(calcFace(a[i]+dx1,b[i]+dy1,c[i]+dx2,d[i]+dy2)<=r[i]){
//他広告と重なっていないか
if(dx1<0||dx2>0||dy1<0||dy2>0){
if(!hitSearch(i,dx1,dy1,dx2,dy2)){
//全て問題ないなら採用する
break;
}
}
//広がっていないので、他広告とぶつかることがない
else break;
}
}
}
}
//スコア計算
double sp=calcScore(a[i],b[i],c[i],d[i],r[i]);
double ep=calcScore(a[i]+dx1,b[i]+dy1,c[i]+dx2,d[i]+dy2,r[i]);
// 温度関数
double temp = st_temp + (en_temp - st_temp) * tm / TIME_LIMIT;
// 遷移確率関数(最大化の場合)
double prob = exp((ep-sp)/temp);
//確率
double rnd=randxorsyosu();
//cout<<sp<<","<<ep<<","<<temp<<","<<prob<<","<<rnd<<endl; //DEBUG
//確率probで遷移
if(prob>rnd){
//乱数を適用
a[i]+=dx1;
b[i]+=dy1;
c[i]+=dx2;
d[i]+=dy2;
//スコアを再計算
nowsco=nowsco-sp+ep;
//cout<<nowsco<<","<<mxsco<<"==="<<sp<<","<<ep<<endl; //DEBUG
//スコアが高くなれば更新
if(nowsco>mxsco){
mxsco=nowsco;
//cout<<nowsco<<endl; //DEBUG
for(int i=0;i<n;i++){
amx[i]=a[i];
bmx[i]=b[i];
cmx[i]=c[i];
dmx[i]=d[i];
}
}
}
}
}
//矩形と点の当たり判定
bool colSqDo(int sx1,int sy1,int sx2,int sy2,int dx,int dy){
return sx1<=dx&&sx2>dx&&sy1<=dy&&sy2>dy;
}
//矩形と矩形の当たり判定
bool colSqSq(int sx11,int sy11,int sx12,int sy12,int sx21,int sy21,int sx22,int sy22){
//矩形の中点からの距離で判定する
double w1=sx12-sx11;
double h1=sy12-sy11;
double w2=sx22-sx21;
double h2=sy22-sy21;
double mx1=(double)sx11+w1/2.0;
double my1=(double)sy11+h1/2.0;
double mx2=(double)sx21+w2/2.0;
double my2=(double)sy21+h2/2.0;
return abs(mx1-mx2)<w1/2+w2/2&&abs(my1-my2)<h1/2+h2/2;
}
//画面外に広告が出てないか判定する
bool OutRange(int i,int dx1,int dy1,int dx2,int dy2){
bool f=false;
if(a[i]+dx1<0||a[i]+dx1>ADSIZE) f=true;
if(b[i]+dy1<0||b[i]+dy1>ADSIZE) f=true;
if(c[i]+dx2<0||c[i]+dx2>ADSIZE) f=true;
if(d[i]+dy2<0||d[i]+dy2>ADSIZE) f=true;
//面積が0以下である場合、長さが0
long long s=(c[i]+dx2-a[i]-dx1)*(d[i]+dy2-b[i]-dy1);
if(s<=0) f=true;
//位置関係が逆転していないか
if(c[i]<=a[i]||d[i]<=b[i]) f=true;
if(f) return true;
return false;
}
//n個の衝突判定を行う
bool hitSearch(int i,int dx1,int dy1,int dx2,int dy2){
bool f=false;
//愚直にn個確認する
for(int j=0;j<n;j++){
if(i!=j&&colSqSq(a[i]+dx1,b[i]+dy1,c[i]+dx2,d[i]+dy2,a[j],b[j],c[j],d[j])){
f=true;
}
}
return f;
}
//提出した際の暫定スコアを計算
//デバッグで使う
void calcSubmitScore(){
long long sum=0;
for(int i=0;i<50;i++){
cout<<"No."<<i<<endl;
inputFile(i);
solver();
long long sc=calcTotalScore();
if(sc==0) cout<<"sc=0"<<endl;
sum+=sc;
}
cout<<sum<<endl;
}
//全広告のPの総和を求める
double calcTotalP(){
double psum=0;
for(int i=0;i<n;i++){
double pi=calcScore(a[i],b[i],c[i],d[i],r[i]);
psum+=pi;
}
return psum;
}
//入力と答えから、スコアを計算する
long long calcTotalScore(){
double psum=0;
for(int i=0;i<n;i++){
if(colSqDo(a[i]-1,b[i]-1,c[i],d[i],x[i],y[i])){
if(OutRange(i)) return 0;
if(hitSearch(i)) return 0;
double pi=calcScore(a[i],b[i],c[i],d[i],r[i]);
psum+=pi;
}
}
long long sum=(1000000000.0*psum+0.5)/n;
return sum;
}
//点数を計算する
double calcScore(int x1,int y1,int x2,int y2, int rs){
int s=calcFace(x1,y1,x2,y2);
return 1.0-pow((1.0-(double)min(s,rs)/(double)max(s,rs)),2);
}
//標準入力で値を受け取る
void inputCin(){
if(scanf("%d",&n)!=1){
//基本とおらない...はず
n=randxor()%200;
}
for(int i=0;i<n;i++){
if(scanf("%d %d %d",&x[i],&y[i],&r[i])!=3){
//基本とおらない...はず
x[i]=randxor()%1000;
y[i]=randxor()%1000;
r[i]=randxor()%1000000;
}
}
}
//標準出力で答えを出す
void outputCout(){
for(int i=0;i<n;i++){
printf("%d %d %d %d\n",a[i],b[i],c[i],d[i]);
}
}
//ファイルから入力する
void inputFile(int no){
FILE *fp;
char fname[256];
string sno="00";
char s[256];
//%02dってした方がよかったね...
if(no/10==0) {
sno+="0";
sno+=(char)(no+'0');
}
else{
sno+=(char)(no/10+'0');
sno+=(char)(no%10+'0');
}
//パスは環境によって変える
sprintf(fname,"C:\\Users\\nullkara\\Downloads\\ded8fd3366b4ff0b0d7d053f553cdb84\\tools\\in\\%s.txt",sno.c_str());
//cout<<fname<<endl; //DEBUG
//読み込めない場合はエラー終了
if ((fp = fopen(fname, "r")) == NULL) {
cout<<fname<<" NOT!!!!"<<endl;
exit(0);
}
//ファイルから値を読み込んでいく
int nc=0;
//行末まで読む
while (fgets(s, 256, fp) != NULL) {
//先頭行は1文字だけ
if(nc==0){
n=atoi(s);
}
//2行目以降は空白区切りの3文字
else{
char s1[256]={0},s2[256]={0},s3[256]={0};
int turn=0;
//splitあった気がしたけど、空白分解をごりごりする
for(int i=0;s[i]!='\n';i++){
if(s[i]==' ') turn++;
else{
if(turn==0) {
char ss[256];
sprintf(ss,"%s%c",s1,s[i]);
strcpy(s1, ss);
}
if(turn==1) {
char ss[256];
sprintf(ss,"%s%c",s2,s[i]);
strcpy(s2, ss);
}
if(turn==2) {
char ss[256];
sprintf(ss,"%s%c",s3,s[i]);
strcpy(s3, ss);
}
}
}
//分解した結果を格納
x[nc-1]=atoi(s1);
y[nc-1]=atoi(s2);
r[nc-1]=atoi(s3);
}
//次の行へ
nc++;
}
//ファイル処理終了
fclose(fp);
}
//時間を測定する
double timeCalc(){
//CPUクロック時間で測定(そのためsleepは入れないようにしよう!)
static auto sc=chrono::system_clock::now();
return (chrono::duration_cast<chrono::microseconds>(chrono::system_clock::now() - sc).count() * 1e-6);;
}
//時間が閾値を超えたら強制終了
void checkTimer(double time){
static int first=0;
//閾値を超えた
if(time>=TIME_LIMIT){
//初回の場合、最終処理へ移行する
if(first==0){
//時間制限を少し伸ばし、初回フラグは変えておく
TIME_LIMIT=4.94;
first=1;
//最大値使用の場合は更新する
if(mxchg!=-1){
for(int i=0;i<n;i++){
a[i]=amx[i];
b[i]=bmx[i];
c[i]=cmx[i];
d[i]=dmx[i];
}
}
//伸ばして得点が上げれるなら伸ばす
largeRect(0);
largeRect(1);
largeRect(2);
largeRect(3);
}
//答えを出力してexitする
outputCout();
//cout<<calcTotalP()/n<<endl; //DEBUG
//cout<<DCOUNTER<<endl; //DEBUG
exit(0);
}
}
//面積を計算する
int calcFace(int x1,int y1,int x2,int y2){
return (x2-x1)*(y2-y1);
}
//Cのrandは遅いので、高速なxor128を使う
//https://shindannin.hatenadiary.com/entry/20121224/1356364040
unsigned int randxor()
{
static unsigned int x=123456789,y=362436069,z=521288629,w=88675123;
unsigned int t;
t=(x^(x<<11));x=y;y=z;z=w; return( w=(w^(w>>19))^(t^(t>>8)) );
}
//0~1のランダムな小数を返す
double randxorsyosu(){
return (double)(randxor()%UINT_MAX)/UINT_MAX;
}
//広告が小さい場合、大きくする
//mode0なら右下に、1なら右上、2なら左下、3なら右下に伸ばす
void largeRect(int mode){
//スコアが小さいものから
vector<pair<int,int>> v;
for(int i=0;i<n;i++){
v.push_back(make_pair(calcScore(a[i],b[i],c[i],d[i],r[i]),i));
}
sort(v.begin(),v.end());
//全広告に対して見ていく
for(int idx=0;idx<n;idx++){
int i=v[idx].second;
double pi=calcScore(a[i],b[i],c[i],d[i],r[i]);
int ansx=0;
int ansy=0;
//まだ伸ばせる余地があるなら
if(calcFace(a[i],b[i],c[i],d[i])<r[i]){
//横幅を変えていく
for(int xi=0;;xi++){
int cd=c[i];
int ad=a[i];
//0,2なら+方向、1,3なら-方向
if(mode%2==0) cd+=xi;
else ad-=xi;
bool f=false;
int sf=calcFace(ad,b[i],cd,d[i]);
//画面外に出たり、他の広告とぶつかるならやめる
if(sf>r[i]) break;
if(cd>ADSIZE) break;
if(ad<0) break;
for(int k=0;k<n;k++){
if(i!=k&&colSqSq(ad,b[i],cd,d[i],a[k],b[k],c[k],d[k])) f=true;
}
if(f) break;
//大丈夫そうなら二分探索する
int left=0;
int right=ADSIZE+50;
while(1){
//閾値を超えたら計算打ち切り
checkTimer(timeCalc());
int mid=(left+right)/2;
bool f2=false;
int bd=b[i];
int dd=d[i];
//0,1なら+方向、2,3なら-方向
if(mode/2==0) dd+=mid;
else bd-=mid;
//違反しているなら、広げる範囲を狭める
for(int k=0;k<n;k++){
if(i!=k&&colSqSq(ad,bd,cd,dd,a[k],b[k],c[k],d[k])) f2=true;
}
if(dd>ADSIZE) f2=true;
if(bd<0) f2=true;
//面積がギリギリ超えない範囲を狙っていく
int sf=calcFace(ad,bd,cd,dd);
if(sf>r[i]) f2=true;
if(f2){
if(right==mid) break;
right=mid;
}
else{
if(left==mid) break;
left=mid;
}
}
//結果を反映
int bd=b[i];
int dd=d[i];
//0,1なら+方向、2,3なら-方向
if(mode/2==0) dd+=left;
else bd-=left;
//答えが大きくなったなら更新
double pif=calcScore(ad,bd,cd,dd,r[i]);
if(pif>pi){
pi=pif;
ansx=xi;
ansy=left;
}
}
}
//二分探索の結果を反映
if(mode%2==0) c[i]+=ansx;
else a[i]-=ansx;
if(mode/2==0) d[i]+=ansy;
else b[i]-=ansy;
}
}
//小さくしながらジャストサイズをさがす
//貪欲のあとでしか動かないので注意(右下に点があること前提の実装)
void shortRect(){
//全広告が対象
for(int i=0;i<n;i++){
//スコア計算
double pi=calcScore(a[i],b[i],c[i],d[i],r[i]);
int xmx=a[i];
//線形探索
for(int xi=a[i]+1;xi<c[i];xi++){
//閾値を超えたら計算打ち切り
checkTimer(timeCalc());
//今の横幅で最適な縦幅
int yi=d[i]-r[i]/(c[i]-xi);
if(yi<0) yi=0;
for(int k=0;k<n;k++){
//他とぶつからないか、ぶつかるなら補正
if(i!=k){
if(colSqDo(xi,yi,c[i],d[i],x[k],y[k])){
yi=y[k]+1;
}
if(colSqSq(xi,yi,c[i],d[i],a[k],b[k],c[k],d[k])){
yi=d[k];
}
}
}
if(yi==d[i]) yi--;
double pif=calcScore(xi,yi,c[i],d[i],r[i]);
if(pif>pi&&colSqDo(xi,yi,c[i],d[i],x[i],y[i])){
xmx=xi;
pi=pif;
}
}
//一番スコアが高くなる座標を採用
int yi=d[i]-r[i]/(c[i]-xmx);
if(yi<0) yi=0;
for(int k=0;k<n;k++){
if(i!=k){
if(colSqDo(xmx,yi,c[i],d[i],x[k],y[k])){
yi=y[k]+1;
}
if(colSqSq(xmx,yi,c[i],d[i],a[k],b[k],c[k],d[k])){
yi=d[k];
}
}
}
if(yi==d[i]) yi--;
a[i]=xmx;
b[i]=yi;
}
}
方針は、貪欲に広告を配置した後に焼きなまし法です。
暫定で48909268593点でした。
以下、各関数の軽い説明です。
solver()
定義された変数modeの値によって解き方を変える関数です。
最後まで2つの解き方のどっちがいいかを切り替えながら考えていました。
solveMinKara()
解き方その1です。
minHaiti()を呼び出した後に、yakinamashi()を呼びます。
minHaiti()
最小の配置を行います。
具体的には、各点の周り1マスを囲うように広告を配置します。
yakinamashi()
焼きなましを行います。
この関数だけではないですが、timeCalc()やcheckTimer(double time)を呼んでTIME_LIMITに指定した秒数になったら計算が打ち切られます。
焼きなましの場合は打ち切られるまで永遠に行います。
largeRect(int mode=0)
各広告を左右上下にスコアが高くなるまで伸ばします。
引数のmodeによって伸ばす方向(右上、左上、右下、左下)が変わります。
yakinamashi()なんかを行った後に、最後に1点でも稼ぐために伸ばしたりします。
shortRect()
各広告を縮めてスコアを高くします。
右下に点がある前提(貪欲の後に使う前提)なので、使用タイミングによってはバグります。
donyoku()
貪欲法を行います。
具体的には、左上にある点(x+yが小さい順)から左上にどんどん伸ばしていきます。
このあとにshortRect()やlargeRect(int mode=0)を呼ぶことで貪欲解法になります。
solveDonKara()
解き方その2です。
donyoku()、shortRect()、largeRect(int mode=0)で貪欲をした後に焼きなましを行います。
今回の提出コードはこっちを使うようにしています。
colSqDo(int sx1,int sy1,int sx2,int sy2,int dx,int dy)
点と四角の衝突判定を行います。
x+0.5,y+0.5を含むかなので、判定式にイコールがついてたりついていなかったりします。
colSqSq(int sx11,int sy11,int sx12,int sy12,int sx21,int sy21,int sx22,int sy22)
四角と四角の当たり判定を行います。
2つの四角の中点を算出し、中点間の距離で判定します。
当たり判定のアルゴリズム(2D 四角×四角) – Qiita
OutRange(int i,int dx1=0,int dy1=0,int dx2=0,int dy2=0)
四角が画面外にあったり、面積が0になったりしてないかを判定します。
hitSearch(int i,int dx1=0,int dy1=0,int dx2=0,int dy2=0)
引数i番目の四角と各四角で衝突がないかを判定します。
calcTotalP()
各広告の合計点数(問題文のpiの値)を算出します。
calcSubmitScore()
50ファイルの入力データを読み込んで暫定スコアを算出します。
ですが、時間打ちきりに対応していないため現状動きません…。
(時間打ち切りを消して、焼きなましの回数を固定にしてやれば動かなくもないですが…)
calcTotalScore()
満足度の総和を求めるのですが、何故かAtcoderで提出した時と合わない欠陥を抱えています。
calcScore(int x1,int y1,int x2,int y2,int rs)
渡された四角の情報と、riの情報から問題文のpiの値を求めます。
四角が点を含んでいないとか、そういうことは考慮していないので注意!
inputCin()
cinと書いてますがscanfで標準入力から値を読み込みます。
※名前変えるの忘れてた><
outputCout()
coutと書いてますがprintfで….><
inputFile(int no)
PC上にある入力ファイルを読み込む値です。
デバッグは基本これで出力した答えを、kenkoooo さんツールで確認していました。
timeCalc()
始めてtimeCalcを呼び出した時間からの経過時間が返ります。
checkTimer(double time)
時間が超過していないかの確認と、超過していた場合の打ち切り処理を行います。
randxor()
焼きなまし法のコツ Ver. 1.3 – じじいのプログラミング (hatenadiary.com)
どうもCのrandは遅いらしいので、上記ブログにあるランダム関数を作成しました。
randxorsyosu()
randxor()は1~の整数値が返りますが、randxorsyosu()は0~1の少数がランダムで返ります。
焼きなましの遷移で使用しました。
calcFace(int x1,int y1,int x2,int y2)
面積を求める関数です。
main()
中にあるmodeで『提出用』『ファイル読み込み用』『全ファイル読み込み用』と入出力の形態が変わります。何度かファイル読み込み用で提出してREくらったので、もっとうまくやりたいですね。
①点数をとりあえず獲得
問題文の読み間違い等がないかを確認するために、必ず点数がもらえるコードを書きました。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int x[n],y[n],r[n];
for(int i=0;i<n;i++){
cin>>x[i]>>y[i]>>r[i];
}
for(int i=0;i<n;i++){
cout<<10000/n*i<<" "<<0<<" "<<10000/n*(i+1)-1<<" "<<10000<<endl;
}
}
ACで391196786点獲得
seed16で以下のような感じです。
かすらなかったみたいで、この入力だと0点ですね。
この答え嬉しいことに、
なんと暫定順位も1位となり、スタートダッシュは良い感じに切れたようです。
※この後、ツインターボのように順位が失速していきますが><
ルールで個人的に気を付けたい点は
- x+0.5,y+0.5を含む広告であること
- 広告は大きすぎても駄目であること
- 広告の辺は接してもいいこと
の3つです。特に一番上の+0.5であることは最後まで苦しめられました。
②貪欲する
Introduction to Heuristics Contest – AtCoder
Introduction to Heuristics Contestで貪欲からの乱択がガイドとして載っていたので今回もその方法を取るようにしました。
貪欲は左上の点からひたすら左上に面積を広げ、後から微調整するようにしました。
提出用コードのdonyoku()です。
seed16で以下のような結果です。
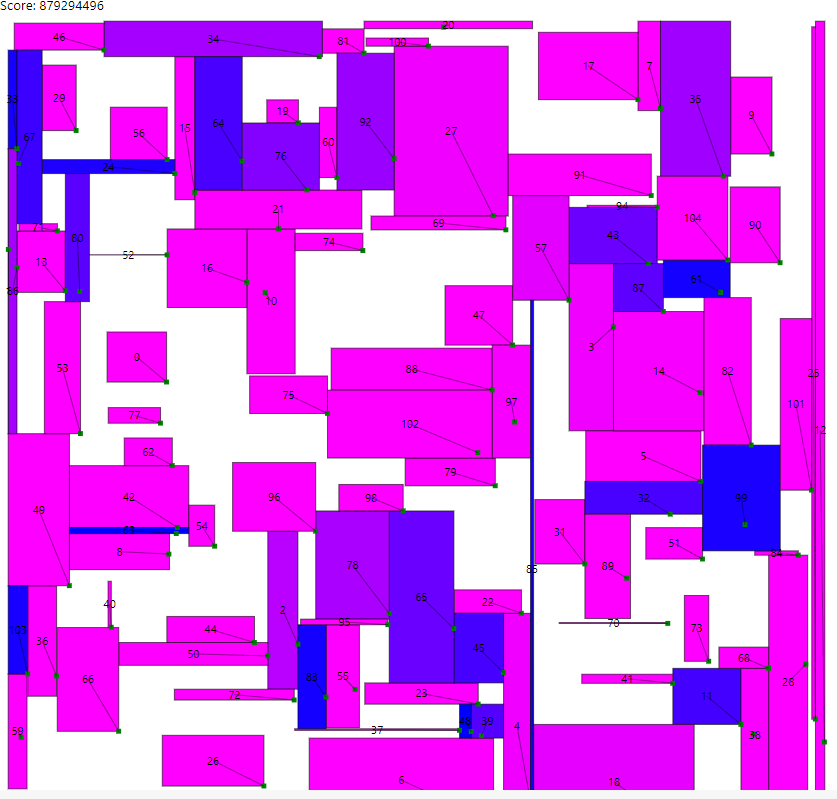
暫定スコアは43754407773くらいでした。
左上にdonyoku()の中の処理で伸ばしていった後に、shortRect()でrに面積が近づくように縮めて調整します。次にlargeRect()で広げて調整します。
画像を見ての通り、広告に対して点が右下の方にあるかと思います。
そして青色の広告(面積が足りていない)が多く、上手く配置できていないことも分かります。
③テスト用の関数の作成
答えの算出に関係ない、手元実行用の関数を作成しました。
提出用コードの場合、
calcSubmitScore()…暫定スコアの計算
inputFile(int no)…noのファイルを入力して読み込む
あたりです。
main関数に定義した変数の値を変えることによって、標準入力かファイル入力か暫定スコアの計算かを切り替えるようにしていました。
※何度かモードの変更忘れでRE出したので、もう少し上手くやりたかったです><
長丁場になるので、こういった便利関数を作るとストレスなくテストができて良かったです。
④山登り法
ランダムに変化させた際に、点数が上がれば変化を採用し、点数が下がればロールバックする…を繰り返すことによってどんどん最適解に近づける方法です。
これを貪欲をした後に、残り時間いっぱいまで行うようにしました。
void waruagaki(){
srand(12345);
int cc=0;
while(1){
cc++;
if(cc%10000==0){
largeRect();
largeRect(1);
}
checkTimer();
for(int i=0;i<n;i++){
int haba=2000;
int dx1=rand()%haba-haba/2;
int dy1=rand()%haba-haba/2;
int dx2=rand()%haba-haba/2;
int dy2=rand()%haba-haba/2;
int ss=(c[i]-a[i])*(d[i]-b[i]);
double sp=1-pow((1.0-(double)min(ss,r[i])/(double)max(ss,r[i])),2);
int es=(c[i]+dx2-a[i]-dx1)*(d[i]+dy2-b[i]-dy1);
double ep=1-pow((1.0-(double)min(es,r[i])/(double)max(es,r[i])),2);
if(ep>=sp-0.1){
if(colSqDo(a[i]+dx1-1,b[i]+dy1-1,c[i]+dx2,d[i]+dy2,x[i],y[i])){
if(c[i]+dx2>=0&&c[i]+dx2<=ADSIZE&&a[i]+dx1>=0&&a[i]+dx1<=ADSIZE&&
d[i]+dy2>=0&&d[i]+dy2<=ADSIZE&&b[i]+dy1>=0&&b[i]+dy1<=ADSIZE){
bool f=false;
for(int j=0;j<n;j++){
if(i!=j&&colSqSq(a[i]+dx1,b[i]+dy1,c[i]+dx2,d[i]+dy2,a[j],b[j],c[j],d[j])) f=true;
}
if(!f){
a[i]+=dx1;
b[i]+=dy1;
c[i]+=dx2;
d[i]+=dy2;
}
}
}
}
}
}
}変化後が違反(範囲外、他の広告とぶつかる等)していなくてスコアが上がれば採用するようにしています。
if(ep>=sp-0.1){と0.1の膨らみを持たせているのは最適ではない局所解に陥るのを防ぐためです。
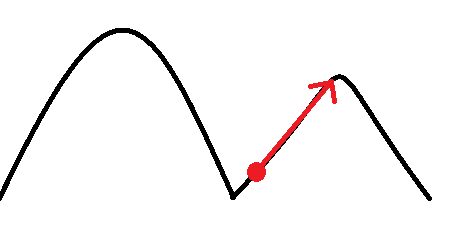
※ある変化をした場合、縦軸のスコアが山のように変わる場合、いい方向にだけ進むと低い山の頂上を目指してしまうことがある(スコアは良くなるが、最大点にはならない)
seed16で実行すると以下のようになりました。

青色がまだ多いですが、詰め詰め感が増したように思えます。
暫定スコアは46388737073でした。
④焼きなまし法
山登り法をした際、最適でない局所解にいくことが問題です。
そういった問題を解決した乱択アルゴリズムが焼きなまし法です。
提出コードのyakinamashi()で実装しています。
double st_temp=0.1;
double en_temp=0.00001;と開始温度と終了温度を設定し、時間経過によって温度を変化させます。
// 遷移確率関数(最大化の場合)
double prob = exp((ep-sp)/temp);で遷移の確率を決定します。
これはスコアが上がれば1.0以上(遷移100%)になり、スコアが下がれば0.0~1.0の値になります。
このとき、tempが小さければ小さいほどexpの結果が小さくなっていきやすくなり、遷移の確率も小さくなります。
つまりは、最初は悪い遷移もある程度受け入れて、最後はあまり悪い遷移を受け入れない。そんな感じになります。
こうすることで、本当の最適解である山を探し出しやすくなります。
seed16で実行すると以下のようになりました。

青い広告がほとんどなくなり、かなり最適に近い配置になっていることが分かるかと思います。
暫定スコアも48809421892とかなり高くなりました。
焼きなまし法には幾つか注意する点があります。
乱択の回数
乱択の回数は多ければ多いほうがいいです。
実行時間は伸ばせないので、1回の乱択にかかる時間を減らすことで回数を増やします。
//スコアを再計算
nowsco=nowsco-sp+ep;再計算の際にn回ループを回さずに、変化した広告の差分だけ足し引きするようにしています。
こうした少しの改善の積み重ねがスコア上昇につながります。
温度
取り得る最高スコアを初期温度、最低スコアを最終温度にするのが基本らしいです。
これは、どれだけ遷移させたいか、どれだけ遷移させるのがいいかで変わってきます。
私は初期温度を0.1と少し下げて悪い遷移を少し抑えるようにしました。
変化の種類
i=count%n;//randxor()%n;
dx1=0;
dy1=0;
dx2=0;
dy2=0;
if(randxorsyosu()>0.90){
int tox=randxor()%haba-haba/2;
int toy=randxor()%haba-haba/2;
dx1=tox;
dy1=toy;
dx2=-tox;
dy2=-toy;
}
else{
double syo=randxorsyosu();
if(syo<=0.3||syo>=0.6){
dx1=randxor()%haba-haba/2;
dx2=randxor()%haba-haba/2;
}
if(syo>0.3){
dy1=randxor()%haba-haba/2;
dy2=randxor()%haba-haba/2;
}
}変化した際に、どのように変化させるかのラインナップを増やした方がいいらしいです。(多分)
ただ闇雲に増やしてもNGで、良い変化をいい感じにさせるのがBESTです。(フワッとしていますね。私は暫定スコアを見ながら調整しました。)
最終提出
計算打ち切りの時間をギリギリまで伸ばしたり、パラメータを吟味しながら提出コードを作成しました。seed16での結果は以下です。
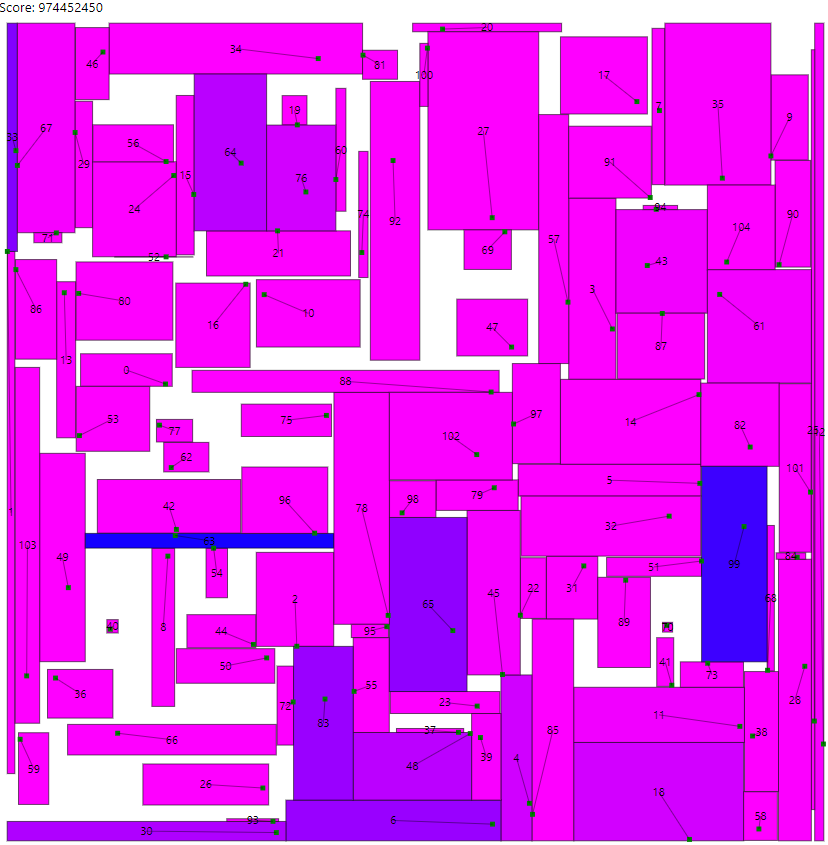
青の広告も1個しかなく、ほぼほぼ最適に配置できていることが分かります。



コメント