はじめに
問題 – AtCoder Beginner Contest 197(Sponsored by Panasonic)
A,B,D,Eの4完でした。
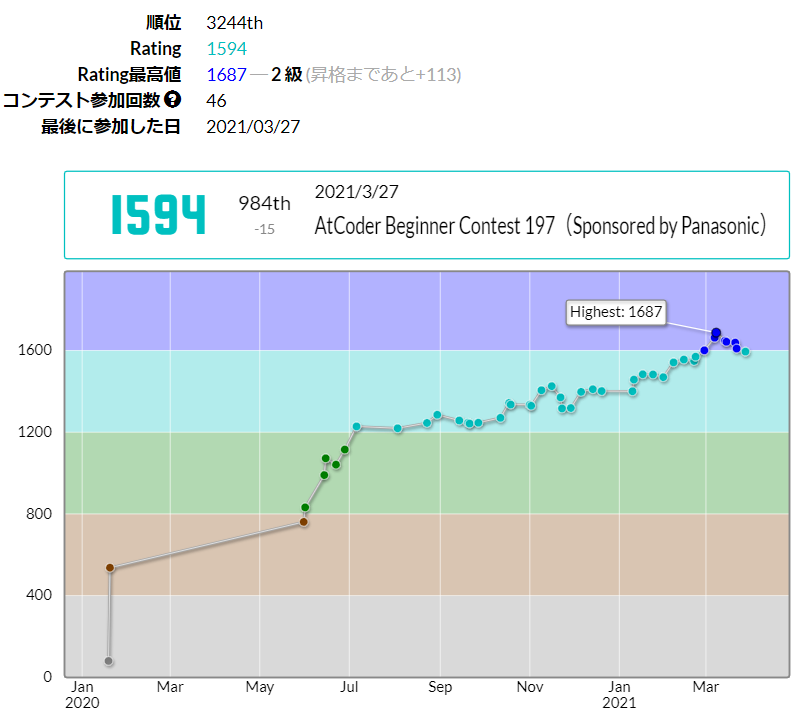
四捨五入すれば青なのでまだセーフです!
今回はCもFもケアレスミスだったので惜しかった問題セットです。
(Dで詰まって焦ったのが敗因です…)
A – Rotate
3文字と決まっているので、出力される文字順は入力に関係なく決まっています。
具体的には、S[1]S[2]S[0]の順番になります。
#include<bits/stdc++.h>
using namespace std;
int main(){
string S;
cin>>S;
cout<<S[1]<<S[2]<<S[0]<<endl;
}B – Visibility
X,Yから4方向に伸ばしていって、画面外か’#’に行くまでのマスの合計をカウントすればOKです。
ゴリゴリ書いていけば良いかと思います。
#include<bits/stdc++.h>
using namespace std;
int main(){
int H,W,X,Y;
cin>>H>>W>>Y>>X;
string S[H];
for(int i=0;i<H;i++){
cin>>S[i];
}
X--,Y--;
int ans=1;
for(int i=X-1;i>=0;i--){
if(S[Y][i]=='#') break;
ans++;
}
for(int i=X+1;i<W;i++){
if(S[Y][i]=='#') break;
ans++;
}
for(int i=Y-1;i>=0;i--){
if(S[i][X]=='#') break;
ans++;
}
for(int i=Y+1;i<H;i++){
if(S[i][X]=='#') break;
ans++;
}
cout<<ans<<endl;
}C – ORXOR
コンテスト中は『連続した区間』が見えていませんでした…。
連続した区間ごとに分けるを言い換えると、任意個の区切りを各数字の間に置くといえます。
区切りの数はN-1個しかなく、Nの最大は20なのでbit全探索で間に合います。
#include<bits/stdc++.h>
using namespace std;
int main(){
int N;
cin>>N;
long long A[N];
for(int i=0;i<N;i++){
cin>>A[i];
}
long long ans=LLONG_MAX;
for(long long i=0;i<(1<<N);i++){
long long ii=i;
vector<long long> v;
v.push_back(A[0]);
for(int j=1;j<N;j++){
if(ii%2==1) v.push_back(A[j]);
else v[v.size()-1]|=A[j];
ii/=2;
}
long long a=0;
for(int j=0;j<v.size();j++){
a^=v[j];
}
ans=min(ans,a);
}
cout<<ans<<endl;
}例えばbit列が0011010の場合、
[A1,A2,A3],[A4],[A5,A6],[A7,A8]
と分けるようにしています。
D – Opposite
難問。大人になればこんなゴテゴテの数学は使わないので苦手です。
(現役でも三角関数やベクトルは苦手だったのでやめてほしい><)
正多角形は円に内接することができ、内接した際に各点の間隔は均等になります。
この問題はこの性質を使います。
#include<bits/stdc++.h>
using namespace std;
int main(){
double N;
cin>>N;
double x0,y0,x2,y2;
cin>>x0>>y0>>x2>>y2;
double xc=(x0+x2)/2,yc=(y0+y2)/2;
double r=sqrt((xc-x2)*(xc-x2)+(yc-y2)*(yc-y2));
double pi=acos(-1.0);
double kaku=atan2(y0-yc,x0-xc)/pi*180;
if(kaku<0) kaku+=360.0;
double ang=kaku+360.0/N;
if(ang>360) ang-=360.0;
double x=r*cos(ang*pi/180);
double y=r*sin(ang*pi/180);
//cout<<kaku<<","<<ang<<endl;
//cout<<xc<<","<<yc<<endl;
//cout<<r<<endl;
//cout<<x+xc<<","<<y+yc<<endl;
printf("%.10f %.10f\n",x+xc,y+yc);
}円に内接した正多角形を考えたときに、入力される2点は180度回転した座標といえます。
そのため、円の中心点=2点の中間、半径=2点の三平方/2となります。
円に内接した多角形の各頂点間の間隔が等しいことから、各頂点間は『360/頂点の数』回した点といえます。
入力される角度はatan2(tanの逆関数)で計算することができるため、0番目の頂点の角度をatan2で求めてから360/頂点数分だけ反時計に回した角度が1番目の頂点の角度になります。
※tanΘはxとyの比率であることから、atanにxとyの比率を入れることでΘを知ることができます。 atan2とは何ぞや?という話ですが、ざっくりxy座標系の角度が知りたいならこっちという認識で問題ないかと思います。(詳しい話は『atan atan2 違い』とかでググってください)
1番目の頂点の角度が分かれば、sin,cosで単位円の座標が分かるため、半径を掛けて今の円での座標に修正すればOKです。
うーーーん、難しい。
E – Traveler
例えば、番号に関係なくボールを取ることを考えると
x=現在位置 .=空きマス n=ボール 1..2.x..3..4 2→3→1→4と左右に振りながら取るのは明らかに無駄だということが分かります。 1-2間を2回、2-x間を4回、x-3間を3回、3-4間を1回...と同じ場所を多くて4回は通っています。 こういった場合の最適は 2→1→3→4、3→4→2→1 のように、片方の端を全て取ってから、もう片方の端を取る方法です。 これ以外は戻る分余計な移動が発生します。
1色しかない場合は、両方のパターン(左端→右端、右端→左端)の最小を取ればいいのですがC色あるとそうはいきません。
ある色だけでは最適でないパターンが、次の色も含めて考えると最適になる可能性があるからです。
ですが、よくよく考えるとパターンが2つしかありません。
なので、右端で終わるパターンと左端で終わるパターンの2つの最小を毎色取っていけばOKです。
具体的には、
右端で終わるパターン=min(前回の右端で終わるパターンから右端で終わるパターンを実施,前回の左端で終わるパターンから右端で終わるパターンを実施)
左端で終わるパターン=min(前回の右端で終わるパターンから左端で終わるパターンを実施,前回の左端で終わるパターンから左端で終わるパターンを実施)
と4通りを試していきます。
#include<bits/stdc++.h>
using namespace std;
int main(){
int N;
cin>>N;
vector<long long> xc[N+1];
for(int i=0;i<N;i++){
long long X,C;
cin>>X>>C;
xc[C].push_back(X);
}
long long rx=0,lx=0,rc=0,lc=0;
for(int i=1;i<=N;i++){
if(xc[i].size()==0) continue;
sort(xc[i].begin(),xc[i].end());
long long xl=xc[i][0];
long long xr=xc[i][xc[i].size()-1];
long long nr=xr,nl=xl;
long long nrc=LLONG_MAX,nlc=LLONG_MAX;
//rx→xr
long long cost=abs(rx-xl);
cost+=abs(xl-xr);
nrc=min(nrc,cost+rc);
//lx→xr
cost=abs(lx-xl);
cost+=abs(xl-xr);
nrc=min(nrc,cost+lc);
//rx→xl
cost=abs(rx-xr);
cost+=abs(xr-xl);
nlc=min(nlc,cost+rc);
//lx→xl
cost=abs(lx-xr);
cost+=abs(xr-xl);
nlc=min(nlc,cost+lc);
//cout<<i<<","<<nrc<<","<<nlc<<","<<nr<<","<<nl<<endl;
rc=nrc;
lc=nlc;
rx=nr;
lx=nl;
}
cout<<min(rc+abs(rx),lc+abs(lx))<<endl;
}F – Construct a Palindrome
F – Construct a Palindrome (atcoder.jp)
回文は前後の文字が同じであるため、スタートとゴールから同時に移動するようなダイクストラを考えればいいです。
具体的には、頂点(n,m)を考えたとき、頂点nと頂点mから出ている辺の中でCが同じものである組み合わせで遷移していけばOKです。スタートは頂点(1,N)です。
(n,m)が同じになる遷移を省くようにすれば、遷移の最大はN^2くらいにしかならず、Nの最大が1000なら間に合います。
#include<bits/stdc++.h>
using namespace std;
int main(){
int N,M;
cin>>N>>M;
vector<pair<int,char>> v[N+1];
for(int i=0;i<M;i++){
int A,B;
char C;
cin>>A>>B>>C;
v[A].push_back(make_pair(B,C));
v[B].push_back(make_pair(A,C));
}
priority_queue<pair<int,pair<int,int>>> pq;
pq.push(make_pair(0,make_pair(1,N)));
set<pair<int,int>> s;
while(!pq.empty()){
int ns=pq.top().second.first;
int ng=pq.top().second.second;
int c=-pq.top().first;
pq.pop();
if(s.find(make_pair(ns,ng))!=s.end()) continue;
s.insert(make_pair(ns,ng));
// cout<<ns<<","<<ng<<","<<c<<endl;
for(int i=0;i<v[ns].size();i++){
int st=v[ns][i].first;
char sc=v[ns][i].second;
if(st==ng){
//cout<<st<<","<<sc<<endl;
cout<<c+1<<endl;
exit(0);
}
for(int j=0;j<v[ng].size();j++){
int gt=v[ng][j].first;
char gc=v[ng][j].second;
if(gt==ns){
//cout<<st<<","<<sc<<","<<gt<<","<<gc<<endl;
cout<<c+1<<endl;
exit(0);
}
if(gc==sc){
if(gt==st){
cout<<c+2<<endl;
exit(0);
}
pq.push(make_pair(-(c+2),make_pair(st,gt)));
}
}
}
}
cout<<"-1"<<endl;
}この問題、本番ではWAでしたが
pq.push(make_pair(-(c+2),make_pair(st,gt)));が抜けていました。
優先度付きキューを使った理由が、コストの低い順に遷移をしたかったからなのですが、C++の優先度付きキューは降順がデフォルトです。
そのため、昇順にするかコストにマイナスを掛けて逆転させないとコストの高い順からになります。
※そもそも遷移がc+2しかないので、ただのqueueでも良かった…
解けていれば水落はなかっただけに悲しいですね。
『優先度付きキューは降順』は家訓にします。
おわりに
覚えてたことが抜けることが多くなったので、そろそろ一旦整理したいですね。
(引っ越しの作業とか、韓国のゲームの翻訳作業とか


この辺のゲームが忙しくて中々時間が…><)



コメント